The Fundamental Theorem of Algebra says that if there is a polynomial that has a degree of n there will be at least one complex zero if n is greater than zero.
 can be used as an example. The degree is one, which is greater than zero so there is at least one complex zero. There is one complex zero in this case that turns out to be 2.
can be used as an example. The degree is one, which is greater than zero so there is at least one complex zero. There is one complex zero in this case that turns out to be 2.The Fundamental Theorem of Algebra can be used to find the Liner Factorization Theorem. This theorem states that if there is a polynomial with a degree of n there will be exactly n liner factors that contain complex numbers.
This can be written as :
The Liner Factorization Theorem expands on the idea of The Fundamental Theorem of Algebra.
is an example of the Liner Factorization Theorem. Even before factoring we know there will be 3 complex zeros because of the Liner Factorization Theorem. This polynomial can be factored into
 which can be further factored into
which can be further factored intoThe solutions are
This helps lead into the next important idea from this chapter, Complex Zeros Occur in Conjugate Pairs. This means that if
These ideas can all be put together when solving an the problem of finding all the zeros of a polynomial. Take
 then because Complex Zeros Occur in Conjugate Pairs you also know that
then because Complex Zeros Occur in Conjugate Pairs you also know that  must be one of the zeros. We also know that there will be four complex zeros because
must be one of the zeros. We also know that there will be four complex zeros because
of the Liner Factorization Theorem.
The complex zeros can be multiplied together and then long division can be used
to find that the polynomial can be factored into
The zeros would then be
Link to long division generator: http://www.emathhelp.net/calculators/algebra-1/polynomial-long-division-calculator/?numer=x%5E4-4x%5E3-5x%5E2%2B2x%5E2-8x-10&denom=x%5E2%2B2&steps=on




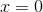











No comments:
Post a Comment