For example:
 has no real solution because there is no real number x that can be squared to produce -1.
has no real solution because there is no real number x that can be squared to produce -1.So, mathematicians created an expanded system of numbers using the imaginary unit i.
Imaginary Unit:
 where
where  .
.By adding real numbers to this imaginary unit, you obtain a set of complex numbers.
If a and b are real numbers, the number a + bi is a complex number.
Standard form of a complex number is a + bi, where a is the real part of the complex
number and the number bi (where b is a real number) is called the imaginary part.
Pictured below are the categories of complex numbers.
Not pictured: Imaginary numbers are outside the domain of "real" but still inside "complex"
Real Numbers: Rational or irrational numbers
Irrational Numbers: Any number that cannot be expressed as a ratio of two integers
Rational Numbers: Recognized as terminating/repeating decimals; Defined as able to be written as a ratio of two integers
Integers: Positive and negative whole numbers
Whole Numbers: All the integers, including 0
Natural Numbers: The positive integers
Equality of Complex Numbers
Two complex numbers a + bi and c + di, written in standard form, are equal to each other if and only if a = c and b = d.
Addition and Subtraction of Complex Numbers
The additive identity in a complex number system is zero.
The additive inverse of the complex number a + bi is -(a + bi) = -a -bi.
Multiplication of Complex Numbers
Use a similar procedure to multiplying two polynomials and combining like terms (FOIL method).
Division of Complex Numbers
To rid an equation of its complex denominator: use complex conjugates.
(This is called realizing the denominator).
Tips about i




And so on.....
To determine the value of i to any power, use long division, and whatever the remainder is, you look to the set of the first four values of i and choose accordingly.












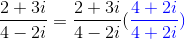





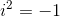


No comments:
Post a Comment