2.3 Real Zeros of Polynomial Functions
The Reason for using Polynomial Long Division and Synthetic Division is to rewrite polynomials into factors in order to simplify.
For Example: we use Polynomial Long Division to simplify 
First, we use our graphing calculators to graph the function.
Next, we find the roots of the function using the graph. x={-1,1/2,2}
We determine that 2 is a zero of the function, this means that the Function can be divided by (x-2) will simplify the equation.
This is when Polynomial Long Division is used.
 Polynomial Long Division is the exact same thing as normal long division, but with polynomials instead.
Polynomial Long Division is the exact same thing as normal long division, but with polynomials instead.
You use Polynomial Long Division by determining what to multiply (x-2) by in order for to be subtracted out, this step keeps repeating until 0 is left to subtract from.
to be subtracted out, this step keeps repeating until 0 is left to subtract from.
Polynomial Long Division is the exact same thing as normal long division, but with polynomials instead.
After Polynomial Long Division, you are left with a more simplified function:
Synthetic Division is an easier, more efficient form of Polynomial Long Division.
For example: simplify using Synthetic Division.
using Synthetic Division.
 First, graph the function to find the roots.
First, graph the function to find the roots.
From the graph, one of the roots is x=2. (The other roots are very complex and very difficult to accurately find on a graph)
Next, you set up the Synthetic Division.
 Since x=2, we place the two outside the "border".
Since x=2, we place the two outside the "border".
The top row of numbers inside of the "border" (2 -1 -7 -3 10) are the coefficients of the function.
The 2 from the first coefficient is brought down under the "border".
Then, the two is multiplied by the root (2), which creates 4. The 4 is added to the -1 above it, which makes 3 that is brought down below the "border". The 3 is then multiplied by 2 which makes 6, then the 6 is added to -7 making -1. The -1 is brought down, and the process is repeated.
The second row of numbers inside of the "border" (4 6 -2 -10) are the coefficients to the simplified function.
The simplified function becomes:
Synthetic Division Tutorial
The Remainder Theorem: If a polynomial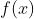 is divided by (x-k), the remainder is
is divided by (x-k), the remainder is

 . For example: if you try to plug in
. For example: if you try to plug in  for
for
and go through synthetic division operations, you get a remainder of 73. This implies
The Factor Theorem: A polynomial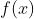 has a factor (x-k) if and only if
has a factor (x-k) if and only if 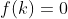 . To help understand this, think of a root; for example: x=2 which implies (x-2)=0, if x=k which would make (2-2)=0, which would prove
. To help understand this, think of a root; for example: x=2 which implies (x-2)=0, if x=k which would make (2-2)=0, which would prove 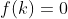 .
.
Next, we find the roots of the function using the graph. x={-1,1/2,2}
We determine that 2 is a zero of the function, this means that the Function can be divided by (x-2) will simplify the equation.
This is when Polynomial Long Division is used.
 Polynomial Long Division is the exact same thing as normal long division, but with polynomials instead.
Polynomial Long Division is the exact same thing as normal long division, but with polynomials instead. You use Polynomial Long Division by determining what to multiply (x-2) by in order for
Notice how the term  is above the term with the same exponent.
is above the term with the same exponent.
If there is a missing term in the function, use  as a placeholder to minimize confusion.
as a placeholder to minimize confusion.
Polynomial Long Division is the exact same thing as normal long division, but with polynomials instead.
After Polynomial Long Division, you are left with a more simplified function:
Synthetic Division is an easier, more efficient form of Polynomial Long Division.
For example: simplify
 First, graph the function to find the roots.
First, graph the function to find the roots.From the graph, one of the roots is x=2. (The other roots are very complex and very difficult to accurately find on a graph)
Next, you set up the Synthetic Division.
 Since x=2, we place the two outside the "border".
Since x=2, we place the two outside the "border".The top row of numbers inside of the "border" (2 -1 -7 -3 10) are the coefficients of the function.
The 2 from the first coefficient is brought down under the "border".
Then, the two is multiplied by the root (2), which creates 4. The 4 is added to the -1 above it, which makes 3 that is brought down below the "border". The 3 is then multiplied by 2 which makes 6, then the 6 is added to -7 making -1. The -1 is brought down, and the process is repeated.
The second row of numbers inside of the "border" (4 6 -2 -10) are the coefficients to the simplified function.
The simplified function becomes:
Synthetic Division Tutorial
The Remainder Theorem: If a polynomial
 . For example: if you try to plug in
. For example: if you try to plug in and go through synthetic division operations, you get a remainder of 73. This implies
The Factor Theorem: A polynomial

No comments:
Post a Comment