In order to sketch the graph of a rational function in the form of:
 and
and  have no common factors, follow this procedure:
have no common factors, follow this procedure:1. - X-Intercepts: Find the solutions the equation:
 (setting the value of the numerator equal to 0). The real solutions to the equation represent the x-intercepts of the graph. (Keep track of any value that has a multiplicity greater than 1).
(setting the value of the numerator equal to 0). The real solutions to the equation represent the x-intercepts of the graph. (Keep track of any value that has a multiplicity greater than 1).2. -Y-Intercept: Find and plot solution to
 which represents the y-intercept on the graph.
which represents the y-intercept on the graph.3. -Vertical Asymptotes: Find the solutions to the equation
 (setting the value of the denominator equal to 0). The real solutions represent the vertical asymptotes of the graph. (Keep track of any value that has a multiplicity greater than 1).
(setting the value of the denominator equal to 0). The real solutions represent the vertical asymptotes of the graph. (Keep track of any value that has a multiplicity greater than 1).4. -Horizontal Asymptote:
a. If the degree of the numerator
 is less than the degree of the denominator
is less than the degree of the denominator  , then the horizontal asymptote is y = 0.
, then the horizontal asymptote is y = 0.b. If the degree of the numerator
 is equal to the degree of the denominator
is equal to the degree of the denominator  , then the horizontal asymptote is the quotient of the leading coefficients.
, then the horizontal asymptote is the quotient of the leading coefficients.c. If the degree of the numerator
 is greater than the degree of the denominator
is greater than the degree of the denominator  there is no horizontal asymptote.
there is no horizontal asymptote.5. - Plot points if position of the curve cannot be found logically.
Example
Sketch the graph of:
X-Intercepts: Solve the equation:  to get x = 0 multiplicity 2, and x = 3. The X-Intercepts of the graph are located at (0,0) tangent to the x-axis & (3,0).
to get x = 0 multiplicity 2, and x = 3. The X-Intercepts of the graph are located at (0,0) tangent to the x-axis & (3,0).
 to get x = 0 multiplicity 2, and x = 3. The X-Intercepts of the graph are located at (0,0) tangent to the x-axis & (3,0).
to get x = 0 multiplicity 2, and x = 3. The X-Intercepts of the graph are located at (0,0) tangent to the x-axis & (3,0).
Vertical Asymptotes: Solve the equation  to get the vertical asymptotes of x = 2 multiplicity 2 & x = -2
to get the vertical asymptotes of x = 2 multiplicity 2 & x = -2
 to get the vertical asymptotes of x = 2 multiplicity 2 & x = -2
to get the vertical asymptotes of x = 2 multiplicity 2 & x = -2
Horizontal Asymptote: The degree of the numerator and the denominator are the same so the horizontal asymptote is equal to the quotient of the leading coefficients. Therefore, the horizontal asymptote is
Plot the point (4,2) on the graph and use logic to draw the remaining curves.
Holes
To graph the function
Example
For the function:

To graph this function, graph the line  and place a hole (represented with an empty circle) on the graph at (2,4)
and place a hole (represented with an empty circle) on the graph at (2,4)
 and place a hole (represented with an empty circle) on the graph at (2,4)
and place a hole (represented with an empty circle) on the graph at (2,4)
Oblique Asymptotes
If the degree of a numerator of a rational function is exactly one more than the degree of the denominator the function has a oblique asymptote.
To find the oblique asymptote use long division to divide the numerator by the denominator.
Example
Use long division to get
- If
 than the curve at x-intercept (b, 0) will be tangent to the x-axis.
than the curve at x-intercept (b, 0) will be tangent to the x-axis. - If
 than both curves at the asymptote x = b head in the same direction.
than both curves at the asymptote x = b head in the same direction.
Helpful Links

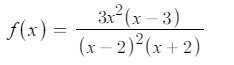





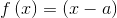









No comments:
Post a Comment