
To be a Polynomial Function…
- "n" has to be a non-negative integer. "n" can be a ...
- Whole Number
- Positive Integer
- The coefficients have to be real numbers
Example of a Polynomial Function

- “n” is a Whole Number
- All coefficients are real numbers
The polynomial
function described above would be a linear function due to its degree of “1”.
If that degree of the function became “2” the polynomial function
would become a quadratic function.
Rules
- a, b, and c are real numbers
Example of a Quadratic
Function

This quadratic function contains a quadratic term (10x2), linear term (25x), and a constant term(-15).
Standard form of a Quadratic Function

Standard
form of a quadratic function can be found by completing the square of the
quadratic function. Having the quadratic function in standard form is very
helpful when it comes to graphing parabolas. In standard form it is easy to
identify the vertex of a quadratic function.
Completing the Square
-
Begin
with the quadratic:
- Simplify
by factoring out a 4:

To complete the square, divide term “b” and multiply the quotient by itself:

Since you can’t just add 4 you must add and subtract 4 to avoid changing the expression:

Now express the equation as a perfect square:

Simplify and distribute the “4” to get Standard Form

From the standard form of this quadratic function you can see that the
x-intercept is (x + 2) being “-2” and the y-intercept is “0”.
Therefore one is able to find out that the vertex of the quadratic function
 is
is  from the standard form.
from the standard form.




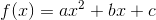
No comments:
Post a Comment