But before we start...
-Putting functions into this standard format will help you figure out the transformations
-Order of transformations matters...sometimes (follow PEMDAS when graphing)
-f(x) and g(x) represent y-coordinates, but remember the f and the g are simply names to differentiate the functions
Today we learned 4 different ways to combine functions:
Let's look at the the two following functions as our base
The first way is addition...
You very simply add g(x) to f(x), order doesn't matter here because addition is commutative, but it is important to remember that you are adding a whole function, not separate terms
The result of the two functions added together is a completely new function, (f+g)(x)
(f+g)(x) has no mathematical significance, it is simply a new name
The second way is subtraction...
This is where it is important to subtract the whole function
Because you must distribute the negative to both terms
Here is the new graph, for (f-g)(x)
The next way is multiplication...
You can probably see where this is going by now
Simply use the foil method to multiply the two functions
The last way is division...
Because we cannot simplify any further, we will leave the function like this
But, we have to determine the domain because we have a variable in the denominator
So, the domain is all real numbers ≠ -5/3
As you can see in the graph of (f/g)(x), there is an asymptote around -1.7, where the x-coordinate would make the function undefined
To sum up the lesson...
This all seems pretty straightforward, but it can become more complicated with different base functions, so remember to follow the rules (distribute all negatives, treat them as whole functions, not individual terms, etc.)!
If you're still confused, check out these Khan Academy videos:
https://www.khanacademy.org/math/algebra2/manipulating-functions/combining-functions/v/sum-of-functions
https://www.khanacademy.org/math/algebra2/manipulating-functions/combining-functions/v/difference-of-functions
https://www.khanacademy.org/math/algebra2/manipulating-functions/combining-functions/v/product-of-functions
https://www.khanacademy.org/math/algebra2/manipulating-functions/combining-functions/v/quotient-of-functions


















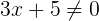








No comments:
Post a Comment