Definition of a Function:
A relation that assigns to each input exactly one output.
An output is another name for y and can also be described as range (set of outputs). Likewise, input is the x also known as the domain (set of inputs). Therefore, in order for something to be considered a function, there has to be exactly one x for a single y or else it's not a function.
Functions can be represented in the four most common ways:
Verbally- a description of words that explain how the input variable is related to the output variable.
Example: The input value are the sides of a square and the output value is the perimeter
Numerically- the use of tables or ordered pairs to represent the relationship between the inputs and outputs
Example: (0, 1), (1, 2), (2, 3), (3, 4)
Graphically- points on a graph in which the input values are represented on the x-axis and the output values are on the y-axis.
This graph represents a function because no input has more than one output value. How can you determine if a graph is a function by just looking at it? What you can do is what's called the Vertical Line Test. You draw a vertical line anywhere on the graph and if the line hits the graph in more than one spot, then it's NOT a function. Therefore, if the vertical line only hits the graph in one spot, it is a function.
Algebraically- by an equation in two variables, most commonly x and y.
Example:
For each value of x, it has exactly one value of y. Therefore, y is a function of x.
Now that we are able to recognize the different ways functions can be represented, let's take a look at determining whether something is a function represented algebraically.
Does this equation represent y as a function of x?
No, this is not a function because the 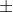 indicates that x has two values of y. Therefore, y is not a function of x.
indicates that x has two values of y. Therefore, y is not a function of x.
 indicates that x has two values of y. Therefore, y is not a function of x.
indicates that x has two values of y. Therefore, y is not a function of x.
Another important part of functions is what we call Function Notation.
Definition of Function Notation:
When representing an equation as a function, it's easier to reference it by renaming it. When you know an equation describes y as a function of x, you can give the function the name of "f".
So if y=1-x, then we can rewrite that in function notation to become f(x)=1-x. The symbol f(x) is read like the value of f at x. Note that the name of the function is f and f(x) is the output value and the input value is x.
Evaluating a function uses function notation to find values of y when given certain x values. Functions have function values that can be shown as f(-1), f(0) and so on. To find these values you have to substitute the input values into the equations.
Example:
Let f(x)=2x-3 and find f(-1)
Plug the value of the input into the equation to find what f(x) is when x is -1.
Peacewise-Defined Functions can also be evaluated.
Example:
Evaluate the function when x=-1, 0, and 1
Since x=0 is greater than or equal to 0, use the equation x-1
Because x=1 is greater than or equal to 0, use the equation x-1

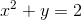

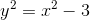


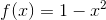


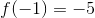
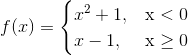




No comments:
Post a Comment