Profoundly Important Thing: y = f(x) . . . The point (x, y) is on the graph of f.
Definition of a function's domain:
The set of input values for which the output values are defined.
Input refers to the independent variable, such as x, and output refers to the function, or f(x). All real inputs must result in real outputs. In some cases, the domain of a function is directly given.
Example:
f: {(-2, 4), (-1, 1), (0, 0), (1, 1), (2, 4)}.
For this function, the domain includes the x coordinates in each of the ordered pairs. Domain = {-2, -1, 0, 1, 2}.
If the function is only defined by an expression, then its domain is implied. It follows the previous definition, which is the set of values for which the function is defined.
Example:
This function is defined when the denominator does not equal 0. Therefore, the domain equals all real numbers expect for 3. This is clear from the function's graph:
Example:
This function is defined when (4 - 2x) is nonnegative. A negative value under the radical would give an imaginary output. Therefore, the domain equals all real numbers less than or equal to 2.
Definition of the difference quotient:
The difference quotient is used in calculus to find the derivative. To evaluate a difference quotient, f(x+h) and f(x) must first be determined.
Example:
When evaluating difference quotients, terms should add to 0 and h should be factored out.
Application problems are an important part of section 1.1.
Example:
a) Write the area of the rectangle as a function of x.
The area of a rectangle is:
The base is equal to 2x and the height is equal to y, so the equation can be rewritten as:
To rewrite the function in terms of x, y can be replaced with the given function of the parabola:
After simplifying, the final answer is:
b) Determine the domain of your function.
Since the base is defined in terms of x, x is positive. x is also less than 3 because of the boundaries set by the parabola. The domain (0, 3) eliminates the possibility of dimensions equal to negative values or zero.
c) Find the maximum area of the rectangle.
The maximum value of 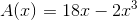 is the maximum area. Using a graphing calculator, graph this function. Since the domain is (0, 3), set 0 as the Xmin value and 3 as the Xmax value.
is the maximum area. Using a graphing calculator, graph this function. Since the domain is (0, 3), set 0 as the Xmin value and 3 as the Xmax value.
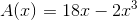 is the maximum area. Using a graphing calculator, graph this function. Since the domain is (0, 3), set 0 as the Xmin value and 3 as the Xmax value.
is the maximum area. Using a graphing calculator, graph this function. Since the domain is (0, 3), set 0 as the Xmin value and 3 as the Xmax value.
Using the calc tool, determine the maximum point. The maximum area is approximately 20.78 units squared.
Parts a and b of this problem are used to solve part c. In the future, problems similar to this may only ask for the maximum area of the rectangle bounded by the given parabola. The steps used above should still be applied.









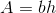

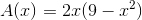

No comments:
Post a Comment