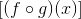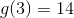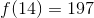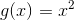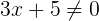1.4: Arithmetic Combinations...Continued

The first thing we learned today is how to find f composed of g of x:

For example:

Findwhen...

Step #1

The first step would be to rewrite as

Step #2

Next you find g(3) by plugging in 3 for every x.

Step #3

Now you use g(3)=14 to find f(g(3)).  Substitute 14 for g(3) and rewrite the equation as f(14) and solve.

Answer: 

Is it commutative?

No (except for a few examples that we will learn later)

We can prove this by...

Solving  and comparing our answer to 

Step #1
The first step would be to rewrite as

Step #2
Next you find f(3) by plugging in 3 for every x.

Step #3

Now you use f(3)=10 to find g(f(3)).  Substitute 10 for f(3) and rewrite the equation as g(10) and solve.

Answer:  is not the same as 

Substitution

You can use  when you are solving problems using substitution.

For example, you can rewrite and solve the equationas where 

Other types of problems

You could also be given  and have to find what f(x) and g(x) are.

For example, find f(x) and g(x) if...

The first step would be to factor the denominator:

The next step is to find the inner function, which is this problem is g(x).  There can be multiple answers to these types of problems, but in this case, the most obvious is:

After finding g(x), you can substitute each x-5 with x.  This would leave you with the equation:

Visit the following websites for more information and examples:

http://www.purplemath.com/modules/fcncomp3.htm

http://www.mesacc.edu/~scotz47781/mat120/notes/composition/composite_functions_intro.pdf

https://www.youtube.com/watch?v=X0NzjXa2SRQ

1.4: Arithmetic Combinations

But before we start...

-Putting functions into this standard format will help you figure out the transformations

-Order of transformations matters...sometimes (follow PEMDAS when graphing)

-f(x) and g(x) represent y-coordinates, but remember the f and the g are simply names to differentiate the functions

Today we learned 4 different ways to combine functions:

Let's look at the the two following functions as our base

The first way is addition...

You very simply add g(x) to f(x), order doesn't matter here because addition is commutative, but it is important to remember that you are adding a whole function, not separate terms 

 

The result of the two functions added together is a completely new function, (f+g)(x)

(f+g)(x) has no mathematical significance, it is simply a new name

The second way is subtraction...

This is where it is important to subtract the whole function

Because you must distribute the negative to both terms

Here is the new graph, for (f-g)(x)

The next way is multiplication...

You can probably see where this is going by now

Simply use the foil method to multiply the two functions

And voilà, you have (f*g)(x)

The last way is division...

Because we cannot simplify any further, we will leave the function like this

But, we have to determine the domain because we have a variable in the denominator

And as we know, if we have a zero in the denominator  undefined

So, the domain is all real numbers ≠ -5/3

As you can see in the graph of (f/g)(x), there is an asymptote around -1.7, where the x-coordinate would make the function undefined

To sum up the lesson...

This all seems pretty straightforward, but it can become more complicated with different base functions, so remember to follow the rules (distribute all negatives, treat them as whole functions, not individual terms, etc.)!

If you're still confused, check out these Khan Academy videos:

https://www.khanacademy.org/math/algebra2/manipulating-functions/combining-functions/v/sum-of-functions

https://www.khanacademy.org/math/algebra2/manipulating-functions/combining-functions/v/difference-of-functions

https://www.khanacademy.org/math/algebra2/manipulating-functions/combining-functions/v/product-of-functions

https://www.khanacademy.org/math/algebra2/manipulating-functions/combining-functions/v/quotient-of-functions