A common thing to learn after polar coordinates is how to graph them to make various graphs such as rose curves, limaçons, circles, and lemniscates. A good way to get comfortable with graphing polar functions is to use a table and plot points the connect the points to form a graph.
Here is the graph of:
You can check the graph by using your graphing utility to graph the equation and see if it matches. Another way to confirm the graph is correct is by changing the equations to parametric mode. The graph of
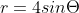
in parametric form is
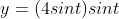
and
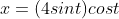
because the graph of a polar equation
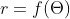
can be changed into parametric form
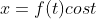
and
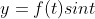
.
The graph of
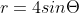
is traced out twice, meaning that the graph is symmetrical to the line
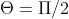
. You can also have symmetry with respect to the polar axis and the pole by replacing the coordinates by either adding a negative or subtracting or adding
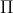
. You can also use symmetry to sketch a graph.
The following is using symmetry to sketch the graph

By replacing
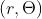
with
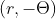
you find out that the graph is symmetric with respect to the polar axis because cosine is an even function.
Here is the graph of

This graph is called a limaçon because of it's shape. Polar graphs can also be rose curves, circles, and lemniscates.
The graph of
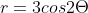
is a rose curve as shown in the figure below:
The graph of
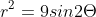
is a lemniscate as shown in the figure below:
The graph of
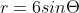
is a circle as shown in the figure below:
You can analyze these graphs by finding the zeros, maximum values, and symmetry.





No comments:
Post a Comment