Definition of a Limit
- If
becomes arbitrarily close to a unique number L as x approaches c from either side, the limit of 
as x approaches c is L.
- Mathematical Notation of a limit:
Finding Limits
In some cases the
is 
, therefore the limit can be found by using direct substitution.
is , therefore the limit can be found by using direct substitution.
However, this method cannot be used for all limits due to the possibility of indeterminate and undefined outputs. In these cases, a graphing calculator or table can be used to evaluate the limit.
Example #1: Evaluate: 
In this case, using the method of direct substitution and solving for 
yields the correct value of the limit, 5.
yields the correct value of the limit, 5.
This value can be verified by using the graph of the function 
Example #2: Evaluate: 
Solving for the value of 
results in 
or indeterminate. Therefore, we must use a table or graph to evaluate the limit.
results in or indeterminate. Therefore, we must use a table or graph to evaluate the limit.
Graphing the function 
yields:
yields: 
Additionally, a table can be made to represent values near 
from looking at the information provided in the graph and table we can see that 
Instances in which a Limit Does Not Exist:
- When finding limits within functions make sure that both sides approach the same number. If they do not, then the limit Does Not Exist.
Example #3: Evaluate:
Graphing the function 
yields:
yields:
From this graph you can see that as x approaches 0 from the right, approaches 1, while as x approaches 0 from the left, approaches -1. Because x does not approach the same number from either side the limit Does Not Exist.
approaches 1, while as x approaches 0 from the left, approaches -1. Because x does not approach the same number from either side the limit Does Not Exist.- In addition, if does not approach a unique number, then the limit Does Not Exist.
Example #4: Evaluate: 
Graphing the function 
yields:
yields:
From this graph you can see that as x approaches 1 from the left and right, increases without bound. Thus, as x approaches 1, tends to infinity. Despite this, 
because 
is not a unique number. Therefore the limit Does Not Exist.
increases without bound. Thus, as x approaches 1, tends to infinity. Despite this, because is not a unique number. Therefore the limit Does Not Exist.
Example #5: Evaluate: 
Graphing the function 
yields
yields
From this graph you can see that as x approaches 0 from the left and right, oscillates between the values 1 & -1. Due to this, the limit Does Not Exist.
oscillates between the values 1 & -1. Due to this, the limit Does Not Exist.
In summary: The limit of as
Does Not Exist if any of these following conditions are met:
- approaches a different number from the right side of c than from the left side of c.
- increases or decreases without bound as x approaches c.
- oscillates between two fixed values as x approaches c.
Additional information about Limits:
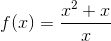
No comments:
Post a Comment