Parametric Equations Definition:
If f and g are continuous functions of t on an interval j, the set of ordered pairs (f(t), g(t)) is a plane curve B. The Equations

are parametric equations
(taken from the text book)
What this means is that for a continuous function, where x, and y can be defined by a third variable, called a parameter and represented by as t. Then it is a parametric equation.
The Purpose of Parametric equations:
If you take for example the distance of a biker from home set at the origin. It will be written as a function of x(horizontal travel) but what if we needed to know where the biker was based on time. It is unnecessary for us to add in a third axis to get a third variable because its path can be modeled on a 2-D plane. This is were setting a parameter and making it a parametric equation gives us the tools necessary to properly model the flight path.
The rectangular equation for a biker moving at 4 ft/s east, and 3 ft/s north and starting at -12,-6 is:
With this equation though you get the bikers y location base on its x location. But this tells us nothing about time, and where the biker is at certain times, with this information we could not answer how long until the biker reaches its house from the location of -12,-9. But if we break up the x, and y vectors into functions of time then we can easily find how long it will take the biker.
The biker is moving at 4 ft/s east which is the x-axis, and moving at 3 ft/s north which is the y-axis. So the rate of change or slope for x is 4 and for y is 3. We can write the functions of x, and y in slope intercept form because they are straight lines.


Now to solve for be, we know at zero seconds the biker's location is at -12,-9. So we plug that point into the equation and solve for b. But we can only plug in the x coordinate into the equation for x and same for y.

Simplify



Simplify


Now we have the parameters for the function based on time the has passed can solve for the original question, how long until the biker reaches the house. Simply set x to zero because that is the x coordinate of the house.


Circles:
Another important role parametric equations play is in graphing circles. If you wanted to graph a circle you can always use.But if you wished to model a circle using parametric equations then you would set the parameters as follows

Now this is only for a circle that starts at (1,0) rotates counter clockwise, has radius of 1, and 1 full rotation is around 6.28 (two pi). With a few easy manipulations we can change the radius, period, and direction of rotation.

Changing k in the equation of x will change the x diameter and will do the same for y if changed in the y function.
The circle below has a radius of 5, because the value of k has been changed to 5 in both equations of x, and y. If it had been changed in only the x equation then the y diameter would be two.
Changing the sign of the function will change the rotation of the circle. + function will rotate counter clockwise, and a - function will rotate clockwise.
Switching sin and cos will change the starting location of the circle.
This is important for modeling a rotating wheel. With using parametric equations one can track the starting point on the wheel and the direction of rotation.
Not all wheels rotate at 1 rotation per two pi seconds. By changing what you multiply theta by can change the rotational speed of the wheel.
The variable h changes the period of one full rotation, where if h is one then the period is two pi.
Extra Resources:
Khan Academy
https://www.khanacademy.org/math/precalculus/parametric-equations
Phils Chatz
http://philschatz.com/precalculus-book/contents/m49409.html
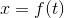







No comments:
Post a Comment