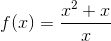12.2 Techniques for Evaluating Limits

Limits of Polynomial Functions 

If p is a polynomial function and c is a real number, then

Limits of Rational Functions 

If r is a rational function given by, and c  is a 

real number such that, then

,.

Evaluating Limits by Direct Substitution 

To use direct substitution:

• the function needs to be continuous.  
• there has to be no values of x that make the function undefined.
• one has to input the limit of x in all values of x to receive an output. 

Example - Evaluate:

Substitute -1 for x

Evaluating Limits by Dividing Out Technique 

When dividing out:

• Factor numerator and denominator.
• Divide out any common factors and simplify.
• Then use direct substitution for x and simplify.

Example - Evaluate: 

Factor numerator

Divide out common factor of x-5

Use direct substitution

Evaluating Limits by Rationalizing Technique 

When using the rationalizing technique:

• Rationalize the numerator of the function.
• Multiply and simplify.
• Then divide out the common factor and simply again. 
• Lastly, use direct substitution to then evaluate the limit. 

Example - Evaluate:

Rationalize the original function with:

Simplify

Divide out common factors

Then use substitution

Simplify

Existence of a Limit

If f  is a function and c and L are real numbers, then



if and only if both the left and right limits exist and are equal to L.

*sorry about the incorrectly formatted functions(the equation editor was not cooperative). 

12.1 Introduction to Limits

Definition of a Limit

• If  becomes arbitrarily close to a unique number L as x approaches c from either side, the limit of as x approaches c is L.

• Mathematical Notation of a limit: 
  

 

 

Finding Limits

In some cases the is , therefore the limit can be found by using direct substitution.

 

However, this method cannot be used for all limits due to the possibility of indeterminate and undefined outputs. In these cases, a graphing calculator or table can be used to evaluate the limit.

 

 

Example #1: Evaluate:

 

In this case, using the method of direct substitution and solving for  yields the correct value of the limit, 5.

 

 

This value can be verified by using the graph of the function

 

 

 

 Example #2: Evaluate: 

 

 

Solving for the value of  results in or  indeterminate. Therefore, we must use a table or graph to evaluate the limit.

 

 

Graphing the function  yields:

 

 

 

 

 

Additionally, a table can be made to represent values near

 

                                                  

              

 

 

 

from looking at the information provided in the graph and table we can see that 

 

 

 

Instances in which a Limit Does Not Exist:

 

• When finding limits within functions make sure that both sides approach the same number. If they do not, then the limit Does Not Exist.

 

 

Example #3:   Evaluate:

 

Graphing the function  yields:

 

 

 

From this graph you can see that as x approaches 0 from the right,  approaches 1, while  as x approaches 0 from the left,  approaches -1. Because x does not approach the same number from either side the limit Does Not Exist.

 

 

 

• In addition, if  does not approach a unique number, then the limit Does Not Exist.

 

 

Example #4:   Evaluate: 

 

 

Graphing the function yields:

 

 

From this graph you can see that as x approaches 1 from the left and right, increases without bound. Thus, as x approaches 1, tends to infinity. Despite this,  because  is not a unique number. Therefore the limit Does Not Exist.

 

Example #5: Evaluate:

 

 

Graphing the function  yields

 

 

 From this graph you can see that as x approaches 0 from the left and right,  oscillates between the values 1 & -1. Due to this, the limit Does Not Exist.

 

In summary: The limit of   asDoes Not Exist  if any of these following conditions are met:

1.  approaches a different number from the right side of c than from the left side of c.
2.  increases or decreases without bound as x approaches c.
3.  oscillates between two fixed values as x approaches c.
 

 

Additional information about Limits:

https://www.khanacademy.org/math/precalculus/limit-topic-precalc/limits-precalc/v/introduction-to-limits-hd