Honors Pre-Calculus A, 3rd Hour, Winter 2016: February 2016

Sunday, February 21, 2016

4.2 Trigonometric Functions: The Unit Circle

The unit circle is a method used to introduce trigonometric functions.

The unit circle is a circle on a x,y coordinate plane with its center on the origin with a radius of 1 unit, hence the name Unit Circle.

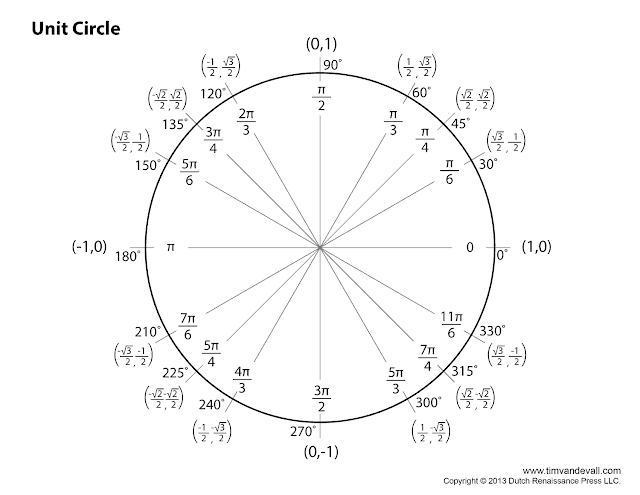
To find a circumference of a circle you use the equation C=2πr, therefore the unit circle has a circumference of 2π. You then can divide the circle into parts of 2π, such as 1/4π, to find the coordinates of a point with that arch length.

To find the x,y coordinates, remember special triangles and their relationship with the Pythagorean theorem.

Given that 360 degrees = 2π, then 30 degrees = 1/6π and 45 degrees= 1/4π

In a 30, 60, 90 triangle any side length will be proportional to each other in this way. This means that when a=1 then the coordinates of a point at 30 degrees will equal

In a 45, 45, 90 triangle any side length will be proportional to each other in this way. This means that when x=1 then the coordinates of a point at 45 degrees will equal

Using this principle, the entire unit circle looks like this.

In the unit circle

where

and

Things to keep in mind...

Also,

and

where c is equal to the measure of an angle of the unit circle, such as 2π.

Above is a periodic function, meaning that

In this function, when c is the smallest true value, c is known as the period of f.

4.1 Radian and Degree Measures

Angles

Trigonometry means "measurement of triangles." Trigonometry deals with the relationships between the sides and angles of triangles.

An angle is determined by rotating a ray about its endpoint. The angle is the measure of rotation. It will have two sides, the initial side and the terminal side. The initial side is the starting position, and the terminal side is the position of the line after the rotation. The vertex is the endpoint of the ray.

A standard position angle is an angle with its initial side on the positive x axis and its vertex on the origin.
angle in standard position

Angles can be positive or negative. A positive angle has counterclockwise rotation, and a negative angle has clockwise rotation.

Image result for positive and negative angles

Angels can be coterminal, when they have the same initial and terminal sides.

Radian Measure

Angles can be measured in degrees or radians.

Definition of a radian: One radian is the measure of a central angle that intercepts an arc s equal in length to the radius r of the circle.

A radian is a measure of rotation just like degrees. A radian, however, is the amount of rotation needed to make the intercepted arc equal to the radius.

The circumference of a circle is equal to 2πr. Therefore, a central angle of one full revolution corresponds to an arc length of s = 2πsr. Because of this, we can conclude that 360° corresponds with 2π.

Because of this, when using radians, there is an easy formula to relate arc lengths to degree measure.

From this, we can derive the equation arc length is equal to the radius length times the measure of the angle join radians.

Cross multiply

Divide by 2π

Monday, February 8, 2016

3.3 Properties of Logarithms

Change of Base Formula

On most calculators, there are only two keys that can be used to simplify a logarithmic expression. The two keys are used to evaluate either common logarithms, which have a base of ten, or natural logarithms, which have a base of e. As a result, the change of base formula is often used to evaluate logarithms to other bases. The change of base formula states that:

$log_{a}x=\frac{log_{b}x}{log_{b}a}$

An Example

It would be impossible to evaluate the original logarithm with most calculators. Using the change of base formula, however, allows the logarithm to be evaluated.

Properties of Logarithms

There are three properties of logarithms. The first states that if two logarithms to the same base of positive real numbers are added together, then their sum equals the logarithm of the product of the two numbers.

The second property of logarithms is much like the first. It states that if one logarithm of a positive real number is subtracted from another logarithm to the same base of another positive real number, the their difference equals the logarithm of the quotient of the second number divided by the first number.

The third property of logarithms states that if a logarithm is taken of a positive real number (u) raised to the power of a real number(n), it is equal to the logarithm of that number (u) multiplied by its exponent (n).

Examples of the Properties of Logarithms

log(4x) = 2

100 = 4x

100/4 = x

25 = x

log x - log 4 = 2

log (x/4) = 2

100 = x/4

100 * 4 = x

400 = x

Verify that:

-ln 1/4 = ln 4

Sunday, February 7, 2016

3.4 Solving Exponential and Logarithmic Equations

Exponential and logarithmic equations can be solved using two strategies based off of the One-to-One Properties and Inverse Properties.

For $a > 0$ and $a \neq 1$ , these properties are true for all $x$ and $y$ for which $log_{a}x$ and $log_{a}y$ are defined.

One-to-One Properties:

1). $a^{x}=a^{y}$ if and only if $x=y$

ex: $5^{x}=125$

$5^{x}=5^{3}$

$x=3$

2). $\mathrm{log}_{a}x= \mathrm{log}_{a}y$ if and only if $x=y$

ex:

$\mathrm{log}_{2}4-\mathrm{log}_{2}x=0$

$\mathrm{log}_{2}4=\mathrm{log}_{2}x$

$x=4$

Inverse Properties:

1). $a^{\mathrm{log_{a}}}x=x$

ex:

$\mathrm{log}x=2$

$10^{\mathrm{log}x}=10^{2}$

$x=10^{2}$

$x=100$

2). $\mathrm{log}_{a}a^{x}=x$

ex:

$\mathrm{log}_{7}7^{x}=4$

$x= 4$

The examples above are the very basic to clearly show how the one-to-one and inverse properties can be used to solve logarithmic and exponential equations. The strategies to solve logarithmic and exponential equations can be summarized through the following:

Rewrite the given equation in a form to use the One-to-One properties of exponential or logarithmic functions.
Rewrite an exponential equation in logarithmic form and apply the inverse property of logarithmic functions.
Rewrite a logarithmic equation in exponential form and apply the Inverse property of exponential functions.

Change-of-Base formula

The Change-of-Base formula shows that: $\mathrm{log}_{a}x=\frac{\mathrm{log_{b}}x}{\mathrm{log}_{b}a}$

This is proved through the following:

let $y= \mathrm{log}_{a}x$

$\mathrm{log}_{b}a^{y}=\mathrm{log}_{b}x$

$y\mathrm{log}_{b}a=\mathrm{log}_{b}x$

$y= \frac{\mathrm{log}_{b}x}{\mathrm{log}_{b}a}$

$\mathrm{log}_{a}x= \frac{\mathrm{log}_{b}x}{\mathrm{log}_{b}a}$

Solving Exponential Equations

Algebraic Solution:

Solve: $8e^{3x}=10$

$e^{3x}=\frac{5}{4}$ divide both sides by 8 and simplify the fraction

$\mathrm{ln} e^{3x}=\mathrm{ln}\frac{5}{4}$ Take logarithm of each side

${3x}=\mathrm{ln}\frac{5}{4}$ Use the inverse property

$x=\frac{1}{3}\mathrm{ln}\frac{5}{4}$ solve for x by multiplying each side by 1/3

Graphical Solution:

Enter $y_{1}=8e^{^{3}x}$ and $y_{2}=10$ into your calculator

use the intersect or zoom and trace features to approximate the intersection point. This graph shows that the two equations intersect at (0.074,10) or $(\frac{1}{3}ln\frac{5}{4},10)$

Graphical Solution 2:

rewrite the original equation as $y_{1}= 8e^{3x}-10$

Use the zero root feature or the zoom and trace features to approximate the x-intercept(s). the zero on this graph is shown at (0.074,0) or $(\frac{1}{3}ln\frac{5}{4},0)$

Solving an Exponential Equation in Quadratic Form:

Algebraic solution:

Solve: $e^{2x}-5e^{x}+4=0$

$(e^{x})^{2}-5e^{x}+4$ Rewrite in quadratic form

$(e^{x}-4)(e^{x}-1)$ Factor

$(e^{x}-4)=0$ $(e^{x}-1)=0$ Set both factors equal to zero

$e^{x}=4$ $e^{x}=1$ isolate ${\color{Red} e^{x}}$

$x= \mathrm{ln}4$ $x= \mathrm{ln}1$

*Check both of these solutions in the original equation to see if either is extraneous*

To find the solutions to this equation graphically, use the second graphical solution method shown above.

Solving Logarithmic Equation

Algebraic Solution:

Solve: $6+ 2\mathrm{log}_{2}x=5$

$2\mathrm{log}_{2}x=-1$ subtract 6 from each side

$\mathrm{log}_{2}x=\frac{-1}{2}$ divide each side by 2

$2^{\mathrm{log}_{2}x}=2^{\frac{-1}{2}}$ exponentiate each side

$x= 2^{\frac{-1}{2}}$ Inverse property to solve

$x=\frac{\sqrt{2}}{2}$

Graphical Solution:

Enter $y_{1}= 6+ 2\mathrm{log}_{2}x$ and $y_{1}= 5$ into your graphing utility

use the intersect or zoom and trace features to approximate the intersection point. This graph shows that the two equations intersect at (0.707, 5). 0.707= $\frac{\sqrt{2}}{2}$

Checking for Extraneous Solutions:

Algebraic Equation:

solve: $\mathrm{ln}(x-2)+\mathrm{ln}(2x-3)=2\mathrm{ln}x$

$\mathrm{ln}\left [ (x-2)\left ( 2x-3 \right ) \right ]=lnx^{2}$ Use the properties of logarithms

$2x^{2}-7x+6=x^{2}$ One-to-One Property

$x^{2}-7x+6=0$ Write in general form

$\left ( x-6 \right )(x-1)=0$ Factor

$x=6$ $x=1$

By checking both of the solutions with the original equation, we can conclude that x=1 is an extraneous answer. This is because the solution x=1 creates the equation $\mathrm{ln}(-1)+\mathrm{ln}(-1)=2\mathrm{ln}1$ , and -1 is outside of the domain of a natural log function.

Graphical Solution:

Rewrite the original equation as $y_{1}=\mathrm{ln}\left ( x-2 \right )+\mathrm{ln}(2x-3)-2\mathrm{ln}$

Use the zero root feature or the zoom and trace features to approximate the x-intercept(s). the zero on this graph is shown at (6,0).

Approximating Solutions

This method should be utilized for equations that contain combinations of algebraic functions, exponential functions, and/or logarithmic functions that will be messy by solving algebraically.

example:

solve: $\mathrm{ln}x=x^{2}-2$