12.3 The Tangent Line Problem
Slope is the rate at which a line rises or falls, but how do we determine the slope for a curve?
Since curves have different rates of rising or falling, different points on the curve have different slopes.
You can determine the slope of a point on a curve by creating a tangent to that point.
A tangent is a line that intersects at only one point.
You can find the tangent line by one of two ways: Approximation or Using the Derivative.
Finding the Tangent line by Approximation can be helpful but it is not accurate, it's just to get an estimate.
For Approximation you choose a point on the curve and estimate the slope by using the point and the point next to it to estimate the rate of change y/x to get the slope. then with the slope you use point slope form (Y-Y1=M(X-X1) then simplify into the standard Y=MX+B to get the formula of the tangent line.
The other, actually accurate way of finding the tangent line is by using the Derivative.
First you must find the difference quotient ((f(x+h)-f(x))/h) of the function of the curve
from the difference quotient you can determine the Derivative(denoted as 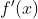 )
)
since the limit is of h going to 0, you substitute 0 in for every h in the simplified formula.
Next, you plug in the x value for the selected point into the Derivative which will give you the slope at that point on the curve.
Finally, use point slope form (Y-Y1=M(X-X1) then simplify into the standard Y=MX+B to get the formula of the tangent line.
For example: Find the tangent of the equation 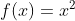 at the point (2,4)
at the point (2,4)
Find the difference quotient 
Simplify 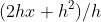
Simplify 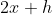
Find the Derivative by substituting in 0 for h for the limit 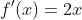
substitute in the x value of the point into the Derivative to find the slope at the point (2,4)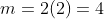
use point slope form then simplify into standard to find the equation of the tangent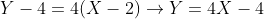



No comments:
Post a Comment