9.3 Geometric Sequences and Series

9.3 Geometric Sequences and Series

Geometric Sequences:

A geometric sequence is a sequence in which from one term to another there is a common ratio.

An example of a geometric sequence is as follows:

As you can see each term in this sequence is multiplied by two to find the next term

                         

Recursive Forms of Geometric Sequences:

All recursive formulas of Geometric Sequences have the a_n term multiplied by a constant number, in order to find the a_n+1 term. Like all recursive formulas, it also needs a point value to start at as well. A very basic example of one could be:

The base formula for a Geometric Sequence in recursive form is:

Where r is the common ratio, and a_n+1 & a_n are terms in the sequence.

To find a term in the sequence using the recursive formula, you need to know the common ratio, and the term that comes before it. In order to find the term before it, you often have to use the formula multiple times which is why for finding the values of terms in a longer sequence I wouldn't recommend using this form. If we knew:

Explicit Forms of Geometric Sequences:

All explicit formulas of Geometric Sequences have the common ratio, raised to the power of a variable. A very basic example of one is:

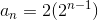
The base formula for a Geometric Sequence in explicit form is:

Where a₁ is the first term in the sequence and r is the common ratio.

Finding the value of a term in a sequence using the explicit form is relatively easy. Once you know the r value and the a₁ term, you can plug and chug to find the n value term. Lets say you know: 

And you want to find what a₇ equals. You'd substitute 7 in for n and just solve from there as follows.

Finding the Sum of Finite Geometric Sequences:
For finding the sum of a geometric sequence, we have a handy formula we can apply:

So to find the sum of a finite series such as:

We can plug in those values into the formula to find the sum:

Finding the Sum of Infinite Geometric Sequences:
Under certain circumstances, it is possible to find the sum of an infinite sequence of numbers. If the common ratio's absolute value is less than or equal to 1, we have another formula to help us find the sum of an infinite series.
if 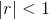 then .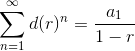

We can use this to find the sum of a multitude of series such as the following one:

And that's pretty much it.