9.3 Geometric Sequences and Series

9.3 Geometric Sequences and Series

Geometric Sequences:

A geometric sequence is a sequence in which from one term to another there is a common ratio.

An example of a geometric sequence is as follows:

As you can see each term in this sequence is multiplied by two to find the next term

                         

Recursive Forms of Geometric Sequences:

All recursive formulas of Geometric Sequences have the a_n term multiplied by a constant number, in order to find the a_n+1 term. Like all recursive formulas, it also needs a point value to start at as well. A very basic example of one could be:

The base formula for a Geometric Sequence in recursive form is:

Where r is the common ratio, and a_n+1 & a_n are terms in the sequence.

To find a term in the sequence using the recursive formula, you need to know the common ratio, and the term that comes before it. In order to find the term before it, you often have to use the formula multiple times which is why for finding the values of terms in a longer sequence I wouldn't recommend using this form. If we knew:

Explicit Forms of Geometric Sequences:

All explicit formulas of Geometric Sequences have the common ratio, raised to the power of a variable. A very basic example of one is:

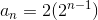
The base formula for a Geometric Sequence in explicit form is:

Where a₁ is the first term in the sequence and r is the common ratio.

Finding the value of a term in a sequence using the explicit form is relatively easy. Once you know the r value and the a₁ term, you can plug and chug to find the n value term. Lets say you know: 

And you want to find what a₇ equals. You'd substitute 7 in for n and just solve from there as follows.

Finding the Sum of Finite Geometric Sequences:
For finding the sum of a geometric sequence, we have a handy formula we can apply:

So to find the sum of a finite series such as:

We can plug in those values into the formula to find the sum:

Finding the Sum of Infinite Geometric Sequences:
Under certain circumstances, it is possible to find the sum of an infinite sequence of numbers. If the common ratio's absolute value is less than or equal to 1, we have another formula to help us find the sum of an infinite series.
if 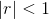 then .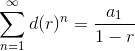

We can use this to find the sum of a multitude of series such as the following one:

And that's pretty much it.

9.1 Sequences and Series

9.1 Sequences and Series

Sequences:

A sequence is a function whose domain is the set of positive integers.

In an infinite sequence, the domain of the function is the set of positive integers
    The function values are as follows:

         

In a finite sequence, the domain of the function is defined as the first n positive integers

To find terms in a sequence you must plug the set of positive integers wherever n may be present and solve for the equation

For example:
     Find the first 3 terms of the sequences given by

 

You now know from the equation that the values imputed are: 

Now just plug in for values of n:

Recursive Sequences:

A recursive sequence is a sequence in which all terms are defined using previous terms.
To find a recursive sequence you must be given one or more of the first few terms.
For example:
     Find the first 3 terms of the sequence defined recursively

Since you are given what is necessary, you may now plug values in and solve the sequence

To continue on and solve forand   you must plug in the previously found answer in the sequence 

Factorials:

Factorials are a type of term that is important to solving sequences

They are as follow:

It is important that you know 

Explicit Sequences:

In explicit sequences, any term may be found without having to know every term before. In the sequence  any integer may be replaced for n to find its value. If you are trying to find  plug 100 in for n and solve: 

A series is defined as the sum of terms in a sequence.

• The sum of all terms in an infinite sequence is called an infinite series
• 
• The sum of a specific terms of a sequence is called a finite sequence
• 

Series can also be expressed using Summation Notation or Sigma Notation  

The examples above can be written as

Where i is the Index of Summation,  and 14 are the Upper Limit of

Summation and 1 and 5 are the Lower Limit of Summation.

Example:

Properties of Sums:

• 

• 
  

• 
  

Note: It is important to keep in mind that one summation may be written in many different ways by rearranging the upper and lower limits of the summation

When the finite series is the sum of the first n terms in a sequence, it is called the nth Partial Sum and is  denoted by which is equal to

Example:

(sum of first 5 terms)

(sum of first 42 terms)

Note: Partial sums can be used to express non partial sum summations

                              
If you are still struggling with Summations, here are a few links you can check out:
http://www.columbia.edu/itc/sipa/math/summation.html
http://www.mathsisfun.com/algebra/sigma-notation.html
http://www.mathsisfun.com/algebra/partial-sums.html
https://www.khanacademy.org/math/integral-calculus/sequences-series-approx-calc/calculus-series/v/partial-sum-notation
https://www.khanacademy.org/math/integral-calculus/sequences-series-approx-calc/calculus-series/v/sigma-notation-sum
https://www.khanacademy.org/math/integral-calculus/sequences-series-approx-calc/calculus-series/v/writing-series-sigma-notation